An Executable Data Structures Cheat Sheet for Interviews
Data Structures Cheat Sheet
This cheat sheet uses the Big O notation to express time complexity.
For a reminder on Big O, see <a href="https://algodaily.com/lessons/understanding-big-o-and-al

Data Structures Cheat Sheet
This cheat sheet uses the Big O notation to express time complexity.
For a reminder on Big O, see Understanding Big O Notation and Algorithmic Complexity.
For a quick summary of complexity for common data structure operations, see the Big-O Algorithm Complexity Cheat Sheet.
Array

Quick summary: a collection that stores elements in order and looks them up by index.
Also known as: fixed array, static array.
Important facts:
Stores elements sequentially, one after another.
Each array element has an index. Zero-based indexing is used most often: the first index is 0, the second is 1, and so on.
Is created with a fixed size. Increasing or decreasing the size of an array is impossible.
Can be one-dimensional (linear) or multi-dimensional.
Allocates contiguous memory space for all its elements.
Pros:
Ensures constant time access by index.
Constant time append (insertion at the end of an array).
Cons:
Fixed size that can't be changed.
Search, insertion and deletion are
O(n). After insertion or deletion, all subsequent elements are moved one index further.Can be memory intensive when capacity is underused.
Notable uses:
The String data type that represents text is implemented in programming languages as an array that consists of a sequence of characters plus a terminating character.
Time complexity (worst case):
Access:
O(1)Search:
O(n)Insertion:
O(n)(append:O(1))Deletion:
O(n)
Dynamic array
Quick summary: an array that can resize itself.
Also known as: array list, list, growable array, resizable array, mutable array, dynamic table.
Important facts:
Same as array in most regards: stores elements sequentially, uses numeric indexing, allocates contiguous memory space.
Expands as you add more elements. Doesn't require setting initial capacity.
When it exhausts capacity, a dynamic array allocates a new contiguous memory space that is double the previous capacity, and copies all values to the new location.
Time complexity is the same as for a fixed array except for worst-case appends: when capacity needs to be doubled, append is
O(n). However, the average append is stillO(1).
Pros:
Variable size. A dynamic array expands as needed.
Constant time access.
Cons:
Slow worst-case appends:
O(n). Average appends:O(1).Insertion and deletion are still slow because subsequent elements must be moved a single index further. Worst-case (insertion into/deletion from the first index, a.k.a. prepending) for both is
O(n).
Time complexity (worst case):
Access:
O(1)Search:
O(n)Insertion:
O(n)(append:O(n))Deletion:
O(n)
See also: same as arrays (see above).
Linked List

Quick summary: a linear collection of elements ordered by links instead of physical placement in memory.
Important facts:
Each element is called a node.
The first node is called the head.
The last node is called the tail.
Nodes are sequential. Each node stores a reference (pointer) to one or more adjacent nodes:
In a singly linked list, each node stores a reference to the next node.
In a doubly linked list, each node stores references to both the next and the previous nodes. This enables traversing a list backwards.
In a circularly linked list, the tail stores a reference to the head.
Stacks and queues are usually implemented using linked lists, and less often using arrays.
Pros:
Optimized for fast operations on both ends, which ensures constant time insertion and deletion.
Flexible capacity. Doesn't require setting initial capacity, can be expanded indefinitely.
Cons:
Costly access and search.
Linked list nodes don't occupy continuous memory locations, which makes iterating a linked list somewhat slower than iterating an array.
Notable uses:
Implementation of stacks, queues, and graphs.
Time complexity (worst case):
Access:
O(n)Search:
O(n)Insertion:
O(1)Deletion:
O(1)
Queue

Quick summary: a sequential collection where elements are added at one end and removed from the other end.
Important facts:
Modeled after a real-life queue: first come, first served.
First in, first out (FIFO) data structure.
Similar to a linked list, the first (last added) node is called the tail, and the last (next to be removed) node is called the head.
Two fundamental operations are enqueuing and dequeuing:
To enqueue, insert at the tail of the linked list.
To dequeue, remove at the head of the linked list.
Usually implemented on top of linked lists because they're optimized for insertion and deletion, which are used to enqueue and dequeue elements.
Pros:
Constant-time insertion and deletion.
Cons:
Access and search are
O(n).
Notable uses:
CPU and disk scheduling, interrupt handling and buffering.
Time complexity (worst case):
Access:
O(n)Search:
O(n)Insertion (enqueuing):
O(1)Deletion (dequeuing):
O(1)
Stack

Quick summary: a sequential collection where elements are added to and removed from the same end.
Important facts:
First-in, last-out (FILO) data structure.
Equivalent of a real-life pile of papers on desk.
In stack terms, to insert is to push, and to remove is to pop.
Often implemented on top of a linked list where the head is used for both insertion and removal. Can also be implemented using dynamic arrays.
Pros:
Fast insertions and deletions:
O(1).
Cons:
Access and search are
O(n).
Notable uses:
Maintaining undo history.
Tracking execution of program functions via a call stack.
Reversing order of items.
Time complexity (worst case):
Access:
O(n)Search:
O(n)Insertion (pushing):
O(1)Deletion (popping):
O(1)
Hash Table
Quick summary: unordered collection that maps keys to values using hashing.
Also known as: hash, hash map, map, unordered map, dictionary, associative array.
Important facts:
Stores data as key-value pairs.
Can be seen as an evolution of arrays that removes the limitation of sequential numerical indices and allows using flexible keys instead.
For any given non-numeric key, hashing helps get a numeric index to look up in the underlying array.
If hashing two or more keys returns the same value, this is called a hash collision. To mitigate this, instead of storing actual values, the underlying array may hold references to linked lists that, in turn, contain all values with the same hash.
A set is a variation of a hash table that stores keys but not values.
Pros:
Keys can be of many data types. The only requirement is that these data types are hashable.
Average search, insertion and deletion are
O(1).
Cons:
Worst-case lookups are
O(n).No ordering means looking up minimum and maximum values is expensive.
Looking up the value for a given key can be done in constant time, but looking up the keys for a given value is
O(n).
Notable uses:
Caching.
Database partitioning.
Time complexity (worst case):
Access:
O(n)Search:
O(n)Insertion:
O(n)Deletion:
O(n)
See also:
Graph
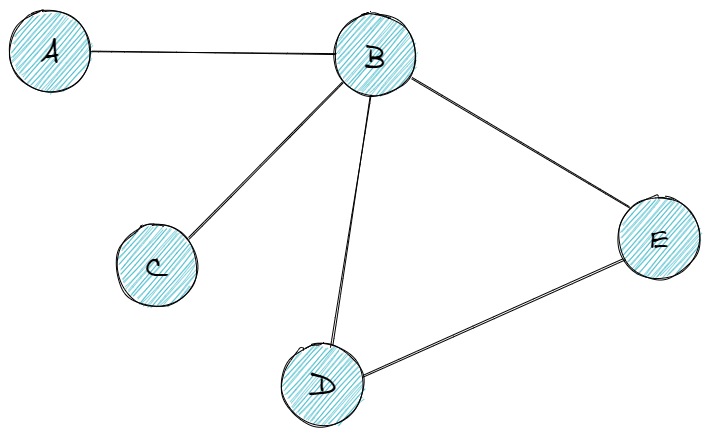
Quick summary: a data structure that stores items in a connected, non-hierarchical network.
Important facts:
Each graph element is called a node, or vertex.
Graph nodes are connected by edges.
Graphs can be directed or undirected.
Graphs can be cyclic or acyclic. A cyclic graph contains a path from at least one node back to itself.
Graphs can be weighted or unweighted. In a weighted graph, each edge has a certain numerical weight.
Graphs can be traversed. See important facts under Tree for an overview of traversal algorithms.
Data structures used to represent graphs:
Edge list: a list of all graph edges represented by pairs of nodes that these edges connect.
Adjacency list: a list or hash table where a key represents a node and its value represents the list of this node's neighbors.
Adjacency matrix: a matrix of binary values indicating whether any two nodes are connected.
Pros:
Ideal for representing entities interconnected with links.
Cons:
Low performance makes scaling hard.
Notable uses:
Social media networks.
Recommendations in ecommerce websites.
Mapping services.
Time complexity (worst case): varies depending on the choice of algorithm.
O(n*lg(n))or slower for most graph algorithms.See also:
Tree
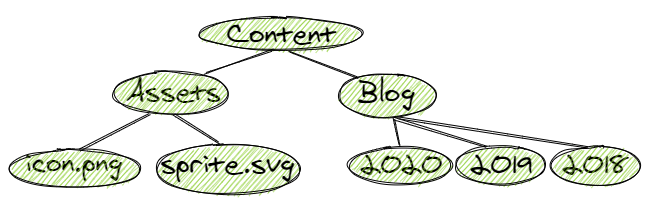
Quick summary: a data structure that stores a hierarchy of values.
Important facts:
Organizes values hierarchically.
A tree item is called a node, and every node is connected to 0 or more child nodes using links.
A tree is a kind of graph where between any two nodes, there is only one possible path.
The top node in a tree that has no parent nodes is called the root.
Nodes that have no children are called leaves.
The number of links from the root to a node is called that node's depth.
The height of a tree is the number of links from its root to the furthest leaf.
In a binary tree, nodes cannot have more than two children.
Any node can have one left and one right child node.
Used to make binary search trees.
In an unbalanced binary tree, there is a significant difference in height between subtrees.
An completely one-sided tree is called a degenerate tree and becomes equivalent to a linked list.
Trees (and graphs in general) can be traversed in several ways:
Breadth first search (BFS): nodes one link away from the root are visited first, then nodes two links away, etc. BFS finds the shortest path between the starting node and any other reachable node.
Depth first search (DFS): nodes are visited as deep as possible down the leftmost path, then by the next path to the right, etc. This method is less memory intensive than BFS. It comes in several flavors, including:
Pre order traversal (similar to DFS): after the current node, the left subtree is visited, then the right subtree.
In order traversal: the left subtree is visited first, then the current node, then the right subtree.
Post order traversal. the left subtree is visited first, then the right subtree, and finally the current node.
Pros:
For most operations, the average time complexity is
O(log(n)), which enables solid scalability. Worst time complexity varies betweenO(log(n))andO(n).
Cons:
Performance degrades as trees lose balance, and re-balancing requires effort.
No constant time operations: trees are moderately fast at everything they do.
Notable uses:
File systems.
Database indexing.
Syntax trees.
Comment threads.
Time complexity: varies for different kinds of trees.
See also:
Binary Search Tree

Quick summary: a kind of binary tree where nodes to the left are smaller, and nodes to the right are larger than the current node.
Important facts:
Nodes of a binary search tree (BST) are ordered in a specific way:
All nodes to the left of the current node are smaller (or sometimes smaller or equal) than the current node.
All nodes to the right of the current node are larger than the current node.
Duplicate nodes are usually not allowed.
Pros:
Balanced BSTs are moderately performant for all operations.
Since BST is sorted, reading its nodes in sorted order can be done in
O(n), and search for a node closest to a value can be done inO(log(n))
Cons:
Same as trees in general: no constant time operations, performance degradation in unbalanced trees.
Time complexity (worst case):
Access:
O(n)Search:
O(n)Insertion:
O(n)Deletion:
O(n)
Time complexity (average case):
Access:
O(log(n))Search:
O(log(n))Insertion:
O(log(n))Deletion:
O(log(n))
Last updated