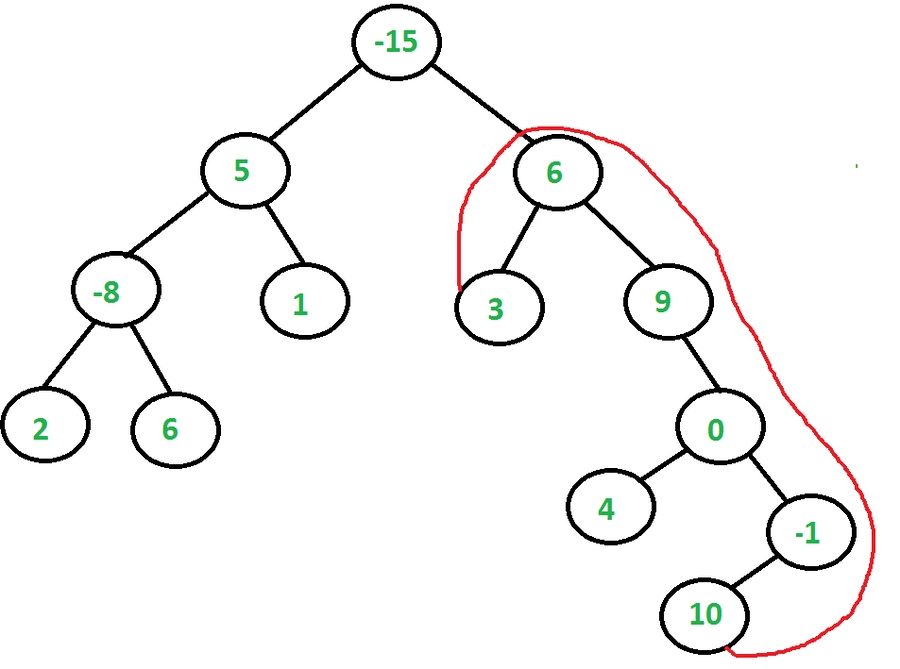
Find the maximum path sum between two leaves of a binary tree

Given a binary tree in which each node element contains a number. Find the maximum possible sum from one leaf node to another. The maximum sum path may or may not go through root. For example, in the following binary tree, the maximum sum is 27(3 + 6 + 9 + 0 - 1 + 10). Expected time complexity is O(n). If one side of root is empty, then function should return minus infinite (INT_MIN in case of C/C++)

Recommended: Please solve it on "PRACTICE" first, before moving on to the solution.

A simple solution is to traverse the tree and do following for every traversed node X. 1) Find maximum sum from leaf to root in left subtree of X (we can use this post for this and next steps) 2) Find maximum sum from leaf to root in right subtree of X. 3) Add the above two calculated values and X->data and compare the sum with the maximum value obtained so far and update the maximum value. 4) Return the maximum value. The time complexity of above solution is O(n2) We can find the maximum sum using single traversal of binary tree. The idea is to maintain two values in recursive calls

(Note: If the tree is right-most or left-most tree then first we have to adjust the tree such that both the right and left are not null. Left-most means if the right of super root of the tree is null and right-most tree means if left of super root of the tree is null.)

1) Maximum root to leaf path sum for the subtree rooted under current node. 2) The maximum path sum between leaves (desired output). For every visited node X, we find the maximum root to leaf sum in left and right subtrees of X. We add the two values with X->data, and compare the sum with maximum path sum found so far.

Python

# Python program to find maximumpath sum between two leaves
# of a binary tree

INT_MIN = -2**32

# A binary tree node


class Node:
    # Constructor to create a new node
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

# Utility function to find maximum sum between any
# two leaves. This function calculates two values:
# 1) Maximum path sum between two leaves which are stored
#    in res
# 2) The maximum root to leaf path sum which is returned
# If one side of root is empty, then it returns INT_MIN


def maxPathSumUtil(root, res):

    # Base Case
    if root is None:
        return 0

    # Find maximumsum in left and righ subtree. Also
    # find maximum root to leaf sums in left and right
    # subtrees ans store them in ls and rs
    ls = maxPathSumUtil(root.left, res)
    rs = maxPathSumUtil(root.right, res)

    # If both left and right children exist
    if root.left is not None and root.right is not None:

        # update result if needed
        res[0] = max(res[0], ls + rs + root.data)

        # Return maximum possible value for root being
        # on one side
        return max(ls, rs) + root.data

    # If any of the two children is empty, return
    # root sum for root being on one side
    if root.left is None:
        return rs + root.data
    else:
        return ls + root.data

# The main function which returns sum of the maximum
# sum path betwee ntwo leaves. THis function mainly
# uses maxPathSumUtil()


def maxPathSum(root):
    res = [INT_MIN]
    maxPathSumUtil(root, res)
    return res[0]


# Driver program to test above function
root = Node(-15)
root.left = Node(5)
root.right = Node(6)
root.left.left = Node(-8)
root.left.right = Node(1)
root.left.left.left = Node(2)
root.left.left.right = Node(6)
root.right.left = Node(3)
root.right.right = Node(9)
root.right.right.right = Node(0)
root.right.right.right.left = Node(4)
root.right.right.right.right = Node(-1)
root.right.right.right.right.left = Node(10)

print "Max pathSum of the given binary tree is", maxPathSum(root)

ck_007)

Output

Max pathSum of the given binary tree is 27