Hashmap or Hash tables
Last updated
Last updated
Many applications require a dynamic set that supports only the dictionary operations INSERT, SEARCH, DELETE. Under reasonable assumptions, the average time to search for an element in a hash table is O(1). The worst case is O(n) when there are as many as n collision when we are doing searching.
A hash table typically uses an array of size proportional to the number of keys actually stored. Instead of using the key as an array index directly, the array index is computed from the key using a hash function. When more than one key maps to the same array index, this is called “collision”, which is usually handled by “Chaining” that we store a linked list in the collide index position.
Hash function
Hash function maps the universe U of keys into the slots of a hashtable T[0..m-1]. With hash function the element is stored in h(k).
h: U -> {0,1,..., m-1}, where the size m of the hash table is much less than |U| . With hash function, the range of array indices and the size of the array is reduced.
Collision
When two keys hash to the same slot, this situation is called collision. The idea to solve collision is to avoid collisions.
One idea is to make h appear to be “random”, thus avoiding collisions or at least minimizing their number. Because |U|>m , there must be at least two keys that have the same hash value; avoiding collisions altogether is therefore impossible. Thus, we use a well-designed, “random”-looking hash function to minimize the number of collisions. However, we still need a method for resolving the collisions that do occur.
Resolving Collision by Chaining
In chaining, we place all the elements that hash to the same slot into the same linked list.Fig 1: Hash table and chaining. Figure from here.
Common Used Hash Functions
A good hash function satisfied the condtion of simple uniform hashing: each key is equally likely to has to any of the m slots.
Step 1: interpreting keys as nature numbers N = {0,1,2, …}. For string or character, we might translate pt as the pair of decimal integers (112,116) with their ASCII character; then we express it as a radix-128 integer, then the number we get is (112*128)+116 = 14452.
Step 2: Define hashing functions
The division method, h(k) = k mod m
The multiplication method, h(k)=⌊m(kA mod 1)⌋. kA mod 1 means the fractional part of kA , which can be noted as {kA} , and equals to kA-⌊ kA ⌋, 0<A<1 . e.g. for 45.2 the fractional part of it is .2.
Implementation with Python List
Python built-in hashmap data structure
The set classes are implemented using dictionaries. Accordingly, the requirements for set elements are the same as those for dictionary keys; namely, that the element defines both __eq__() and __hash__(). As a result, sets cannot contain mutable elements such as lists or dictionaries. However, they can contain immutable collections such as tuples or instances of ImmutableSet. For convenience in implementing sets of sets, inner sets are automatically converted to immutable form, for example, Set([Set(['dog'])]) is transformed to Set([ImmutableSet(['dog'])]).
OrderedDict
Standard dictionaries are unordered, which means that any time you loop through a dictionary, you will go through every key, but you are not guaranteed to get them in any particular order.
The OrderedDict from the collections module is a special type of dictionary that keeps track of the order in which its keys were inserted. Iterating the keys of an orderedDict has predictable behavior. This can simplify testing and debugging by making all the code deterministic.
defaultDict
Dictionaries are useful for bookkeeping and tracking statistics. One problem is that when we try to add an element, we have no idea if the key is present or not, which requires us to check such condition every time.
The defaultdict class from the collections module simplifies this process by pre-assigning a default value when a key does not present. For different value type it has different default value, for example, for int, it is 0 as the default value.
Time Complexity for Operations
Search, Insert, Delete: O(1). Check here for more details.
Stacks and queue are dynamic lists in which the element removed from the list by the DELETE operation is prespecified. The operation of PUSH and POP takes O(1) time complexity. These two structure are good for problems that we deal with element in either FIFO or LIFO manner.
queue: it is first in, first out, FIFO, which can be used to implement iterative BFS. The following code is the basic implementation with Python.
stack: the element deleted is the most recently inserted, Last in first out, LIFO, which can be used to implement iterative DFS. The following code is the basic implementation with Python.
Deque (operation from both side): In Python, the deque class from the collections module is a double-ended queue. It provides constant time opearations for inserting ore removing items from its beginning or end. It can be used to implement both stack and queue structure we mentioned above and usually is more time efficient than the above implementation. Mainly because inserting or removing elements from the head of a list takes linear time.
Heap
As we can see we can implement either the max-heap or the min-heap as an array. Because the tree is complete, the left child of a parent (at position p) is the node that is found in position 2_p_ in the list. Similarly, the right child of the parent is at position 2_p_+1 in the list. To find the parent of any node in the tree, we can simply use Python’s integer division. Given that a node is at position n in the list, the parent is at position n/2.
There are two kinds of binary heaps: max-heaps and min-heaps. In both kinds, the values in the nodes satisfy a heap property. For max-heap, the property states as for every node i other than root.
Thus, the largest element in a max-heap is stored at the root.
For a heap of n elements the height is theta(logn) because it is a complete binary tree.
Heap can be used into heapsort and a priority-queue data structure. Operations include:
MAX-HEAPIFY, runs in O(lgn), is the key to maintaining the max-heap property
BUILD-MAX-HEAP, runs in linear time, produces a maxheap from an unordered input arrary
MAX-HEAP-INSERT, HEAP-EXTRACT-MAX, HEAP-INCREASE-KEY, and HEAP-MAXIMUM, runs in O(lgn) time, allow the heap data structure to implement a priority queue.
heapq: heapq from collections is an implementation of heap, which can be used to maintain a priority queue. Operations include heappush, heappop, and nsmallest. heapq in python to maintain a priority queue with O(logn)
Items are removed by the highest priority or say the lowest number first. Also, accessing the 0 index of the heap will return the smallest item.
More materials can be found here.
Monotonous Stack: For monotonous increasing stack, which only allow the increasing element to be put in the stack, smaller one came will kick out the larger one in the previous position, untill we found one that is smaller than the current element. For the monotonous decreasing stack, the larger elements will force the stack to kick out the previous smaller element untill larger one found. In monotonous stack, we only operate at the end of the stack. To summarize, monotonous stack has two features:
monotonic
when adding new element, we will delete all the previous elements that break the first monotonic feature.
For increasing stack: we can find the first element to the left that is larger than current element
For decreasing stack: we can find the first element to the left that is smaller than current element.
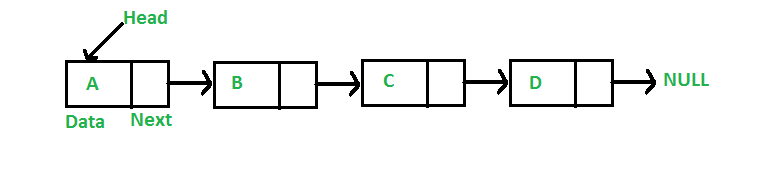
Why Linked List? Arrays can be used to store linear data of similar types, but arrays have following limitations. 1) The size of the arrays is fixed: So we must know the upper limit on the number of elements in advance. Also, generally, the allocated memory is equal to the upper limit irrespective of the usage. 2) Inserting a new element in an array of elements is expensive, because room has to be created for the new elements and to create room existing elements have to shifted.
Advantages over arrays 1) Dynamic size 2) Ease of insertion/deletion
Drawbacks: 1) Random access is not allowed. We have to access elements sequentially starting from the first node. So we cannot do binary search with linked lists. 2) Extra memory space for a pointer is required with each element of the list.
For Linked List, we can only iterate over elements, for python code example:
Dummy Node in Linked List
Remove Duplicates from Sorted List II
Reverse Linked List II
Partition List
Basic Linked List Skills
Sort List
Reorder List
Two Pointers in Linked List (Fast-slow pointers)
Merge K Sorted Lists
Binary Tree and Binary Search Tree, please see my following post.Solving Tree Problems on LeetCodePart of this great node comes from blog:medium.com
[1] Cormen, Thomas H. Introduction to algorithms. MIT press, 2009.
[2] Géron, Aurélien. Hands-on machine learning with Scikit-Learn and TensorFlow: concepts, tools, and techniques to build intelligent systems. “ O’Reilly Media, Inc.”, 2017.
[3]https://www.geeksforgeeks.org/heap-queue-or-heapq-in-python/
The (binary) heap data structure is an array that we can view as a nearly complete binary tree. The tree is completely filled on all levels except possibly the lowest, which is filled from left up to a point.(a) binary tree (b) an array
Like arrays, Linked List is a linear data structure. Unlike arrays, linked list elements are not stored at contiguous location; the elements are linked using pointers.
